ジニ不純度
決定木の不純度の指標として使用される「ジニ不純度」の説明している以下の文章のXXXとYYYに当てはまる組みとして正しいものを選べ
ある2つのカテゴリー(ラベル0とラベル1)を持つ特徴量を分割する場合のジニ不純度は、ラベル0なのにラベル1と割り振られる確率とラベル1なのにラベル0と割り振られる確率のXXXを考える必要がある。クラス0である確率をP(0)、クラス1である確率をP(1)とすると、求めるジニ不純度は
となる
XXX = 和, YYY = 2
シグモイド関数
シグモイド関数について説明している以下の文章のうち、正しいものを選べ
ニューラルネットワークの活性化関数として使われる関数であり、この関数の出力は0より大きく1より小さい
不定積分
以下の不定積分の答えとして正しいものを選べ。Cは積分定数とする。
pandasデータフレームdfをNumPy配列に変換する処理として正しいものを選べ。
正解
df.values# np.exp(), np.exp()
以下のコードを実行した場合の出力として、正しいものを選べ。
import numpy as np
np.log(np.exp(np.eye(2)))
array([[1., 0.], [0., 1.]])eyeメソッドで2行2列の単位行列を作成します。
続いてここに指数関数のexpメソッドを実施します。結果は次のようになります。array([[2.71828183, 1.], [1., 2.71828183]])
これはe(ネイピア数)の1乗は2.71828183になることと、eの0乗は1になるからです。
最後に対数を取ります。底をeとした対数がeの場合、1が出力され、底をeとした対数が1の場合0が出力されます。
numpy.exp()
numpy.exp(x) は指数関数 ex を返します。
np.log(a)
底をeとするaの対数
np.log2(a)
底を2とするaの対数
np.log10(a)
底を10とするaの対数
np.log1p(a)
https://python.atelierkobato.com/exp/#outline__2_2
https://www.sejuku.net/blog/70027
read_csv(usecols=[カラム名])
csvファイルをpandasで読み込む場合に、読み込むカラムを指定する方法として正しいものを選べ
※選択肢中の’data.csv’ は読み込む元データが格納されたcsvファイルとする
正解
pd.read_csv(‘data.csv’, usecols=[カラム名])
正規表現 re.match()),
enjoyという出力を返すように、XXXXに当てはまるものとして正しいものを選べ
import re
pattern = r"enjoy"
text = "enjoy data science"
matchOB = re.match(pattern , text)
if matchOB:
print(matchOB.XXXX)
group()
文字列の先頭がマッチするかチェック、抽出: match()
先頭に限らずマッチするかチェック、抽出: search()
文字列全体がマッチするかチェック: fullmatch()
https://note.nkmk.me/python-re-match-search-findall-etc/
マッチした文字列を取得: group()
https://note.nkmk.me/python-re-match-object-span-group/
サポートベクターマシンのハイパーパラメーターのC
scikit-learnのサポートベクターマシンのハイパーパラメーターのCについて説明している以下の文章のうち正しいものを選べ
正解
Cの値が小さいほど、マージンは大きくなる
https://qiita.com/sz_dr/items/f3d6630137b184156a67
コストパラメータは, 誤分類をどの程度許容するかを決めるパラメータです.
はSVMが解く2次計画問題の式に現れます.
C
が小さいほど誤分類を許容するように,
大きいほど誤分類を許容しないように超平面を決定します.
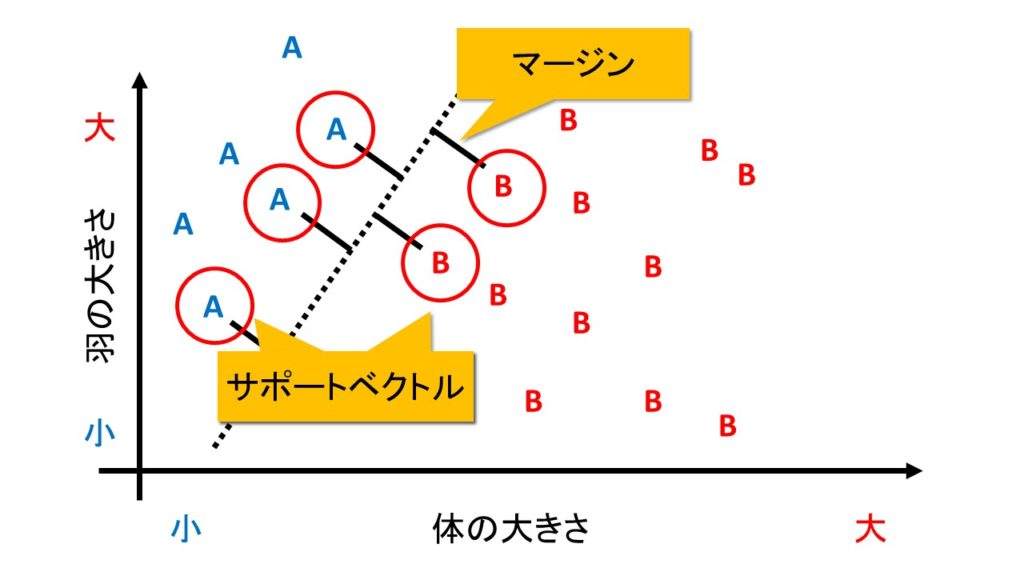
SVMでは、正しい分類基準を見つけるために、「マージン最大化」という考えを使います。
マージンとは、「判別する境界とデータとの距離」を指します。
これが大きければ、「ほんの少しデータが変わっただけで誤判定してしまう」というミスをなくすことができます。
なお、境界線と最も近くにあるデータを「サポートベクトル」と呼びます。
境界の近くにあるデータは、言い換えると「A種かB種か微妙」な位置にあるデータだとみなせます。
そんな「どっちか分けにくいやつら」が多いと困りますね。
なので、境界とデータとの距離、すなわちマージンを大きくするようにして誤判別を防ぐのです。
逆にいれば、誤判別を防ぐには「境界の近くにあるデータ」だけあれば十分です。
明らかに、ハッキリと分かれる奴らをいちいち考える必要はありません。
なので、境界の近くにあるデータ、すなわちサポートベクトルのみを用いて分類を行います。
サポートベクトル以外のデータの値が多少変化したとしても、分類のための境界線の位置は一切変わりません。
「手持ちのデータ」に対して無理に適合性を高めてしまい、「まだ手に入れていないデータ」への予測精度が下がってしまう問題を「過学習」と呼びます。
過学習をせずに予測ができることを「汎化性」と呼び、この汎化性能を高めるために、あえて誤分類を許すように工夫します。
誤判別を許すことを前提としたマージンのことを「ソフトマージン」と呼びます。
ソフトマージン君は以下の2つを満たすように頑張ります。
・境界線とデータとはなるべく離れていたほうがいい
・誤判別はなるべく少ないほうがいい
そこで、以下の値を最小にするようにします。
パラメタ「C」という怪しげなのが出てきました。
これは「誤判別をどこまで許容するか」を現すパラメタです。
パラメタCが大きければ、誤判別は決して許さないし、逆にCが小さければ、誤判別はあまり気にしません。
パラメタCが∞に大きかった場合は「誤判別は1回も許さない」という強い制約となり、実質ハードマージンと変わらなくなります。
パラメタCが小さければ、多少誤判別があっても上記の式の合計は大きくならないので「誤判別を許しやすくなる」わけです。
パラメタCは人間があらかじめ決めてやる必要があります。
このように「あらかじめ与えられていることが前提のパラメタ」のことを「ハイパーパラメタ」などと呼びます。
パラメタCはとりあえずテキトーに決めるしかありませんが、グリッドサーチなどを使って「最も予測精度が高くなるようにパラメタをチューニングする」技術もあります。
これは後ほど解説します。
https://logics-of-blue.com/svm-concept/
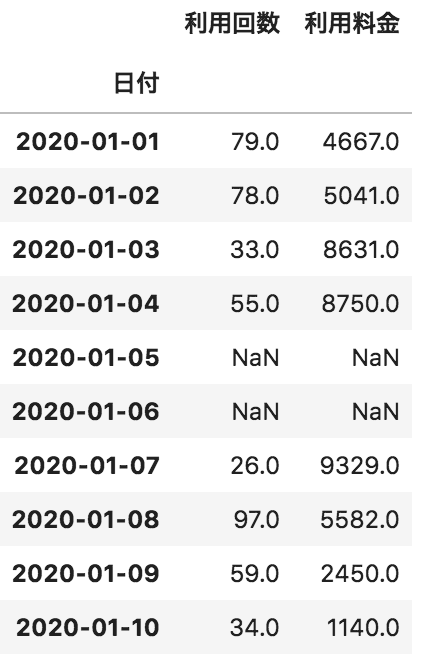
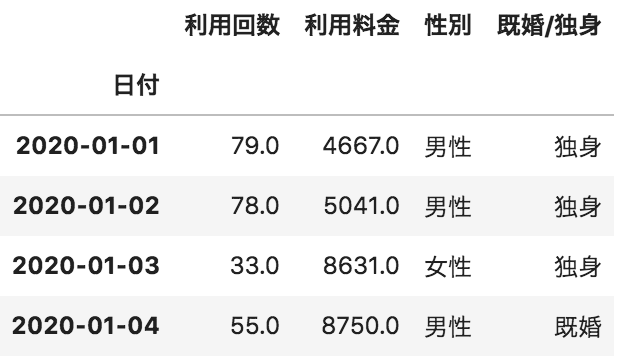
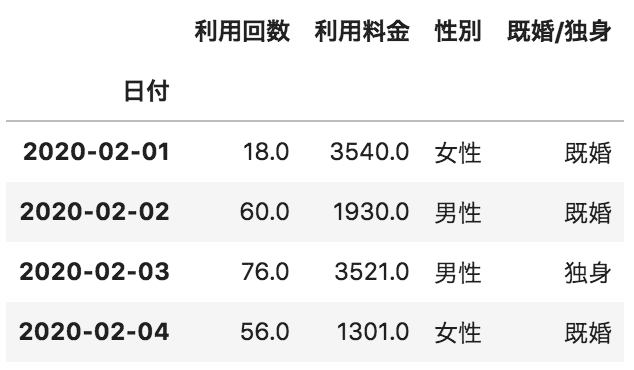
value_counts()
df[“利用回数”].value_counts().to_frame()
value_counts関数
それぞれの値の出現回数を数え上げてくれる関数です。
https://deepage.net/features/pandas-value-counts.html
# アダマール積 np.multiply() メソッド
アダマール積の具体例

https://mathlandscape.com/hadamard-prod/
https://www.delftstack.com/ja/howto/numpy/element-wise-multiplication-python/
行列の積 np.matmul() メソッド
https://qiita.com/renesisu727/items/6ef7ff8f61fe16b4c505#:~:text=%E5%89%B2%E6%84%9B%E3%81%97%E3%81%BE%E3%81%99%E3%80%82-,%E8%A1%8C%E5%88%97,-%E3%81%AE%E7%A9%8D%E3%81%AB%E3%81%A4%E3%81%84%E3%81%A6
行列の積について
np.matmulを用いれば行列の積を計算できます。
np.dotでも二次元配列においては同様の挙動を示しますが、次元により細かい挙動が違うので、二次元以下の場合はこちらの記事を、三次元以上の場合はこちらの記事を参考にしてください。
しかし、ここで気をつけなければならないのが、一次元のarrayは縦ベクトルと横ベクトルを区別しないということです。
行列の掛け算を行うときには、通常線形代数でもそうであるように次元に注意する必要がありますが、一次元配列は縦ベクトルと横ベクトルを区別しないため、多少ガバガバでも計算できてしまうのです。
以下の例で確認しましょう。
array1 = np.array([[1, 1],
[1, 1]])
array2 = np.array([1, 1])
result = np.matmul(array1, array2)
print(array1.shape)
print(array2.shape)
print(result.shape)(2, 2)
(2,)
(2,)
正規化
特徴量の正規化とは、特徴量の大きさを揃える処理のことです。
特徴量の桁数が大きく異なるもの同士を使って分析を行なった場合、特徴量の大きな値が分析結果に大きく影響を与えてしてしまい、逆に特徴量の小さなデータが分析結果に反映されなくなってしまいます。
このような特徴量の偏りを無くし、同じ基準でデータを評価できるようにしたい場合、前処理の工程で特徴量を正規化します。
特徴量の正規化の代表的な手法として、分散正規化と最小最大正規化とがあります。
分散正規化
分散正規化は、特徴量の平均値が0、標準偏差が1になるよう特徴量を変換する手法です。
分散正規化には、scikit-learnのpreprocessingモジュールのStandardScalerクラスを使用します。
最小最大正規化
最小最大正規化は、特徴量の最大値が1、最小値が0になるように特徴量を変換する手法です。
最小最大正規化には、scikit-learnのpreprocessingモジュールのMinMaxScalerクラスを使用します。
# 要素の取得
以下のコードを実行した場合の出力として、正しいものを選べ。
import numpy as np
A = np.array([[0, 1, 2, 3, 4]])
B = np.full((1, 5), 1)
A[A>=B]
array([1, 2, 3, 4])
ここでは条件を満たす要素の取得をしています。A>=Bの条件を満たすものは正解の選択肢になります。
A[A>=B] ←要素の取得。真偽ではない。
drop メソッド
concatメソッドでaxis=0を設定するとindex方向(行)に結合します。
参考:DataFrameを横方向に結合する concat、merge、join-python
SQL の join のように DataFrame を横方向につなげる場合、使用可能な関数(or メソッド)は3つあります。
concat
merge
join
どれを使うかは結合キーをなににするかで変わります。データをキーにして結合したければ merge を使います。インデックスで結合したければ、動きは微妙に違いますが3つのうちどれでも使えます。
ちなみに、concat は縦方向の結合もできます。
次元削減(Dimensionality Reduction)
上図上は身長と体重の関係を示したグラフです。
このグラフにおいて、プロットされている×は体格を示したもので、右上方向に進むほど、体格が良いととらえることができます。
それを一次元の線上に落とし込んだものが上図下の赤い直線になります。
この状態でも、右へ進むほど体格が良くなっている、と認識することができるかと思います。
今回の例は、二次元から一次元に落とし込んでいますが、削減後も体格を示すというデータの意味を保つことができています。
この場合、赤い直線は「体格」の軸と呼ぶことができるでしょう。
次元削減とは、多次元からなる情報を、その意味を保ったまま、それより少ない次元の情報に落とし込むことです。
https://qiita.com/aya_taka/items/4d3996b3f15aa712a54f
主成分分析(Principal Component Analysis:PCA)
Irisデータセットは3種類の150個のデータがある4次元のデータセットなので、出力は(150, 4)となります。
続いて、主成分分析によって、2次元に変換してみます。
# 主成分分析による次元削減
pca = PCA(n_components = 2, whiten = False)
pca.fit(X)
X_pca = pca.fit_transform(X)
print(X_pca.shape)
変換後にはIrisデータセットは150個のデータがある2次元のデータセットとなっているので、出力は(150, 2)となります。
さらに、このデータは2次元のデータなので、matplotlibを用いることで、これらを可視化することが出来ます。
n_components = 2
→2次元に削減 という意味
pickleモジュール
選択肢③ pickleモジュールは、Pythonのオブジェクトをシリアライズしてファイルなどで読み書きできるようにすることができ、標準出力をバッファリングして制御するために便利である。
pickleモジュール
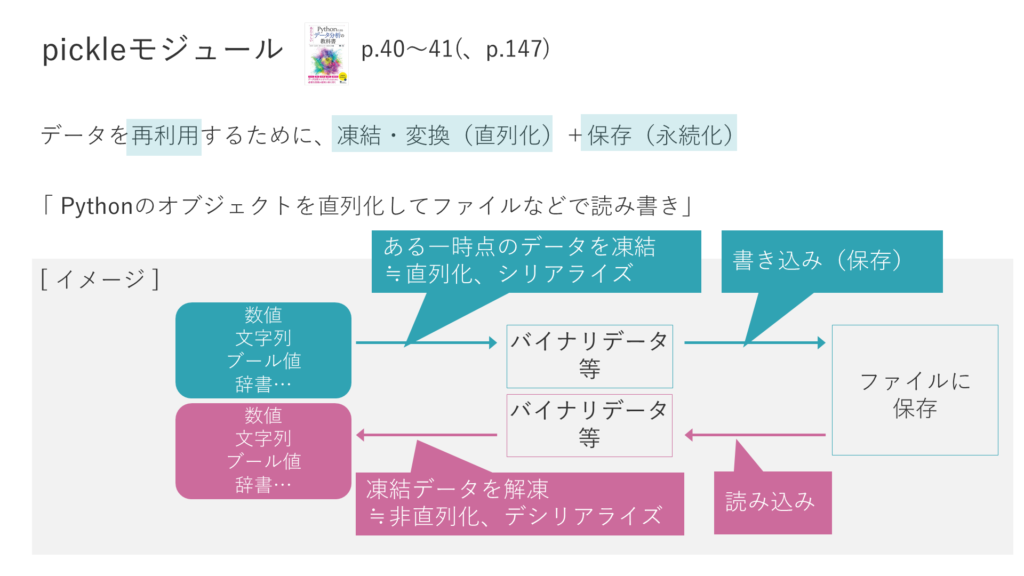
pickleモジュールというのは、「データを再利用するために、データの凍結・変換(直列化)と保存(永続化)」一度に行う仕組みです。
通常、プログラムで生成したデータは、プログラムの終了時に消えます。プログラムの終了後もそのデータを利用したい時などにpickleを使います。

選択肢③は、後半の「標準出力をバッファリングして制御するために便利である」の部分が誤っています。
「標準出力をバッファリングして制御する」ということをするのは、pickle(Python)ではなくPHP、具体的にはPHPのアウトプットバファリングです。右図はPHPのアウトプットバファリングの処理イメージです。
通常、PHPプログラムでechoすると、コンソール上にそのままhello worldと出力されますが、より長い複雑な文字列などのときに、コンソールへの出力を制御したい場合があります。
こうした場合にアウトプットバファリングで、バッファに一時保存しておき、バッファにためてからコンソールやファイルに出力します。これが「標準出力をバッファリングして制御する」ということです。先ほど見ました「pickleによるシリアライズと保存」という処理とは全く異なります。
# バイナリデータの読み込み、書き込み

選択肢④は誤りの肢です。文章中のメソッド名が間違っています。正しくは、read_pickle、to_pickleです。
# 行列とベクトルの積
選択肢③は、正しい肢です。
行列Aは3×2行列で2列、ベクトルxの要素数が2なので、掛け算ができます。結果は要素数3のベクトルとなります。

NumPyに関する次の記述のうち、誤っているものはどれか。
NumPy配列のスライスでは、リストやタプルのスライスのようにスクエアブラケットの重ねがけはしないようにと述べました。その理由を解説します。スライスで抽出した配列は、元々の配列のコピーではなくビューです。つまり、メモリに格納されている元々の配列の値を参照しています。
# 行と列の数が異なる配列同士の四則演算(ブロードキャスト)
行と列の数が異なる配列同士の演算では、足りない行と列の値が自動的に補われます。これをブロードキャストといいます。
例えば、次のコードをご覧ください。
import numpy as np
array1 = np.array([[1, 2], [3, 4]])
array2 = np.array([10, 20])
array3 = array1 + array2
print(array3)
このように、array2 の足りない行に、そのまま要素の値がスライドされて、演算が行われます。下図をご覧頂くと分かりやすいでしょう。
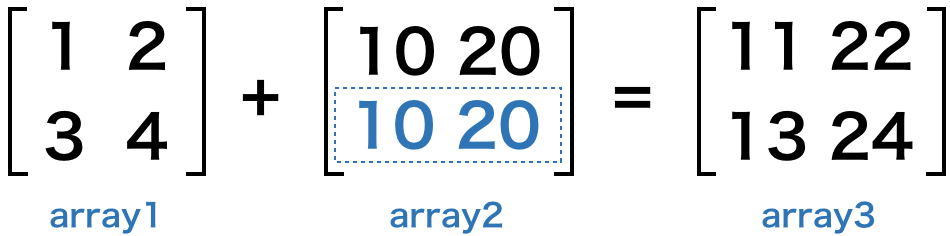
ただし、ブロードキャストは、演算を行う配列同士が、少なくとも行数か列数のどちらかが同一である必要がありますので、覚えておきましょう。
ブロードキャストのルール
ブロードキャストとは、自動で同じ形状にそろえる機能ですが、どんな配列同士も形状がそろえられる訳ではありません。
ブロードキャストとは、以下の2つのルールに従って配列の形状をそろえます。このルールを理解していなければ、ブロードキャストの機能を使いこなせません。なお、赤字の部分が注意する点です。
- 次元の長さが1の部分を複写し自動で長さをそろえる
- 配列の前方に自動で長さ1の次元を追加する
xとyは、次元の長さが1の部分を複写し長さをそろえることで形状をそろえることができます。具体的には下図のように[8, 9]を複写し、yの0番目の次元を1→4にします。
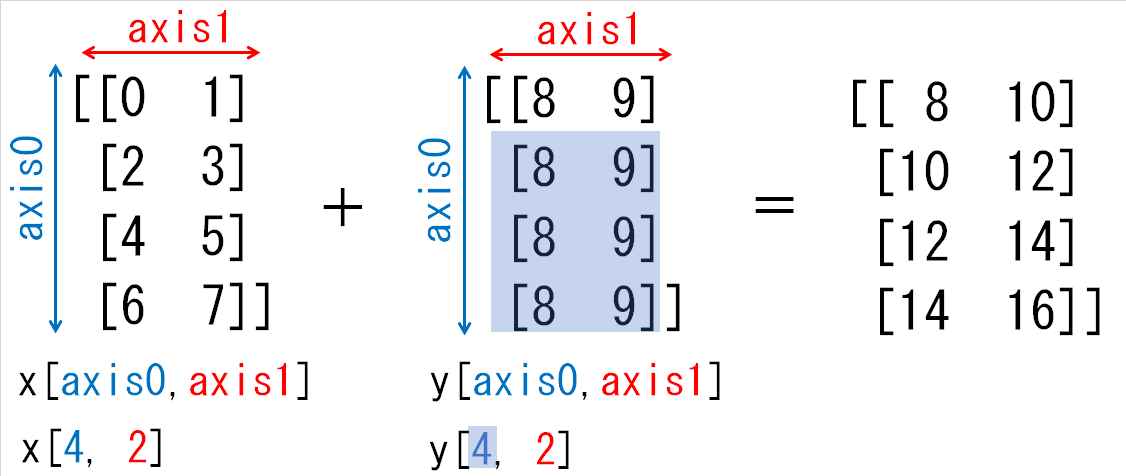
(2) 形状(4, 2)と形状(3, 2)の配列の和
形状(4, 2)の配列xと形状(3, 2)の配列yの和ではブロードキャストの機能は働きません。なぜなら、次元の長さが1の部分がないからです。
実際、yの要素を複写して次元をそろえようとしても次元の長さが1ではないため難しいことがわかります。
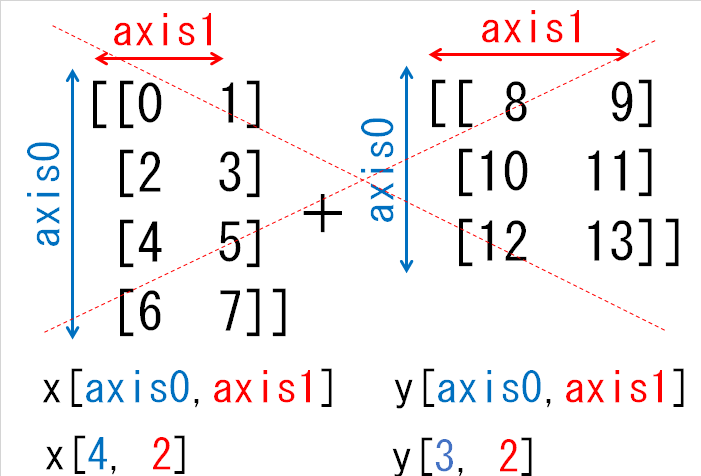
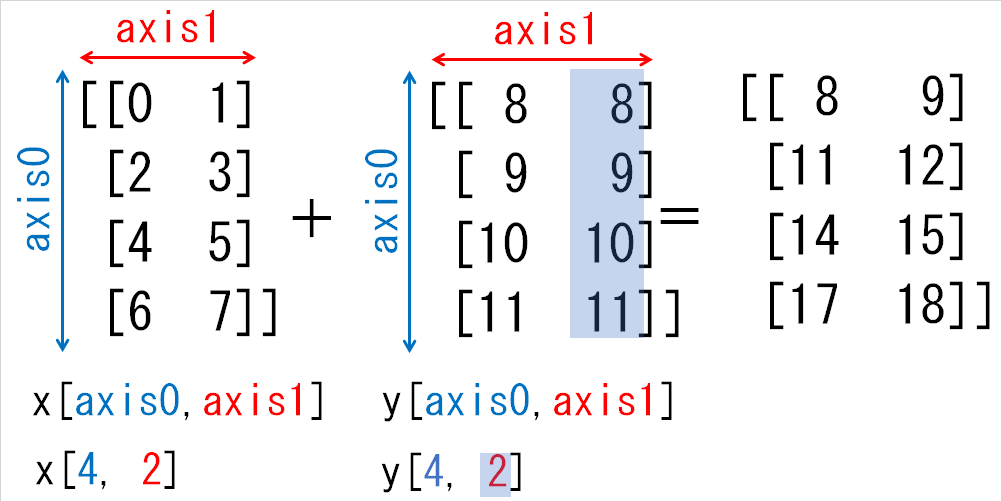
(4) 形状(4, 2)と形状(4, 1)の配列の和
次に形状(4, 2)の配列xと形状(4, 1)の配列yの和を考えてみましょう。これは、yの1番目の次元の長さが1であるため、これを2にすれば形状をそろえられます。
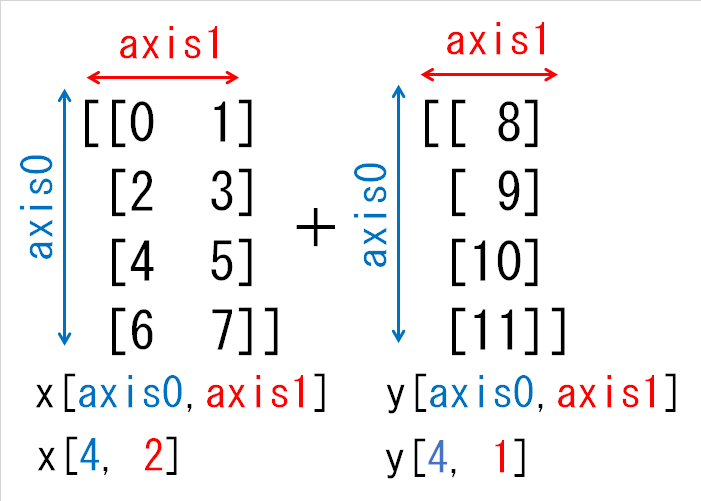
下の図のように、同じ値を複写することによって形状をそろえます。